Работа электропривода характеризуется в первую очередь механической характеристикой двигателя ? = f (М) или n = f (М).
Для двигателя постоянного тока также часто используют электромеханические характеристики ? = f (Iя) или n = f (Iя), где ?, n, Iя, М — соответственно угловая скорость, частота вращения, сила тока якоря и вращающий момент двигателя. Механические характеристики можно рассчитывать как в абсолютных, так и в относительных единицах. Для двигателей постоянного тока наибольшее распространение получил расчет характеристик в относительных единицах.
При расчетах в относительных единицах за базисные величины принимают номинальные данные двигателя Iя, Мном, Uном, nном. Иногда в качестве базисных принимают величины, отличающиеся от номинальных (например, момент статической нагрузки). Величины, выражаемые в относительных единицах, в дальнейшем будут обозначены знаком.
Сопротивления главной цепи в относительных единицах определяют в долях номинального сопротивления.. Под номинальным понимают такое сопротивление цепи якоря, которое при неподвижном якоре и номинальном расчетном напряжении Uном обусловливает номинальную силу тока в якоре:
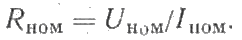
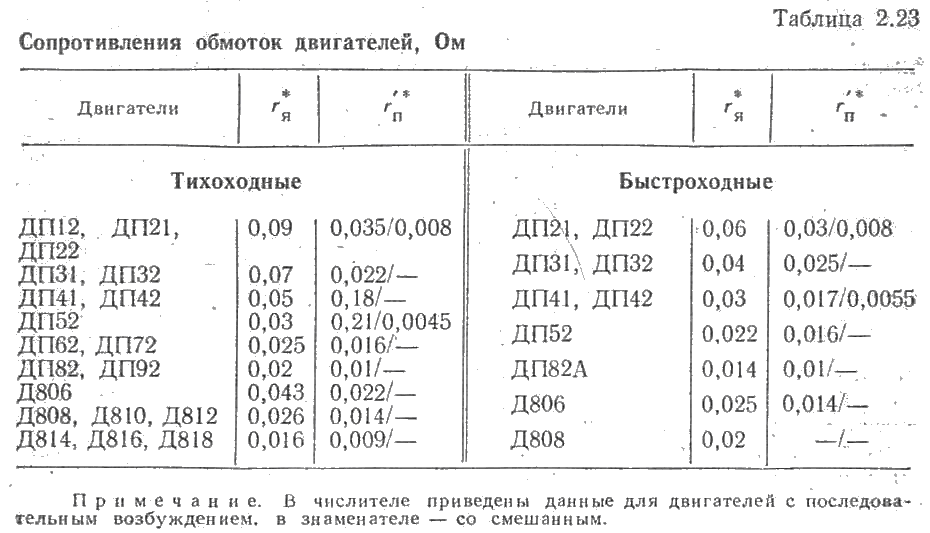
Сопротивление цепи якоря складывается из внутреннего и внешнего сопротивлений. Значения внутреннего сопротивления обмоток двигателей серий ДП и Д в долях номинального при ПВ = 25 % приведены в табл. 2.23. В графе rя* указано сопротивление якоря и дополнительных полюсов двигателей, а в графе r’n* — сопротивление обмотки двигателей последовательного возбуждения. Сопротивление стабилизирующих обмоток двигателей параллельного возбуждения настолько мало, что им можно пренебречь. При расчете типовых характеристик для группы двигателей сопротивление обмоток следует определять как среднее арифметическое значений, приведенных в соответствующих строках табл. 2.23.
Расчет механических характеристик двигателей в относительных единицах приведен ниже и является универсальным. Этот метод расчета пригоден для различных способов возбуждения и соединения обмоток.
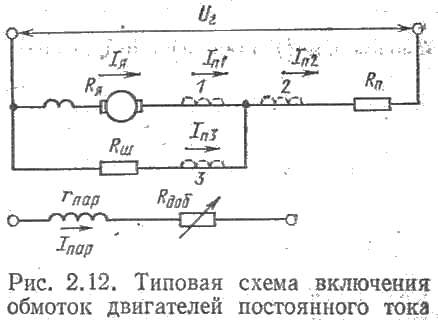
Схема включения двигателя изображена на рис. 2.12, на котором показаны три варианта (1, 2, 3) включения обмоток последовательного возбуждения. Сила тока в этих обмотках обозначена через Iп1, Iп2, Iп3. Обмотка параллельного возбуждения в общем случае получает питание от независимого источника с напряжением Uв.
При расчете механических характеристик, как правило, используют известные схему включения обмотки последовательного возбуждения, сопротивления последовательной и шунтирующей цепей Rп и Rш, напряжение источника питания цепи якоря (главной цепи) Uг, МДС обмотки параллельного возбуждения и соотношение между МДС обмоток последовательного и параллельного возбуждения при номинальной нагрузке. Напряжение Uг может иметь независимое от нагрузки значение Uг — const (сеть постоянного тока). При применении вращающихся или статических преобразователей энергии задают внешнюю характеристику этих преобразователей Uг = f (I) (I — сила тока нагрузки).
МДС главных полюсов двигателя обусловлена суммарным действием электрического тока в обмотках возбуждения, расположенных на этих полюсах. Поскольку номинальная МДС, принятая за базисную, складывается из МДС обмотки параллельного возбуждения и МДС обмотки последовательного возбуждения или стабилизирующей обмотки, то можно принять, что МДС обмотки параллельного возбуждения в относительных единицах будет составлять 0,5 для двигателей серий ДП и Д смешанного возбуждения и 0,9 для двигателей серий ДП и Д параллельного возбуждения. На долю обмотки последовательного возбуждения или стабилизирующей обмотки будет приходиться остальная часть МДС. Учитывая, что эта часть соответствует МДС при протекании номинального тока, для любой силы тока МДС обмотки последовательного возбуждения можно выразить следующими формулами:
для двигателей серий ДП и Д смешанного возбуждения,
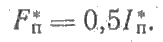
где I*п — сила тока, протекающего по обмотке последовательного возбуждения;
для двигателей параллельного возбуждения со стабилизирующей обмоткой серий ДП и Д
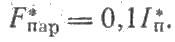
Полная МДС главных полюсов выражается в виде алгебраической суммы МДС обмоток последовательного и параллельного возбуждения:
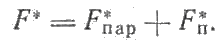
В некоторых случаях для реализации повышенных (пониженных) частот вращения двигателей МДС обмотки параллельного возбуждения берут меньше (больше) номинальной.
Общий метод расчета механической характеристики двигателей постоянного тока в рассматриваемой схеме (см. рис. 2.12) включения заключается в нахождении зависимостей F* = f (Iя*) и Iп* = f (Iя*) и последующем переходе к зависимости n* = f (М*).
Зависимость силы тока в последовательной обмотке от силы тока якоря двигателя устанавливают по одному из следующих уравнений:
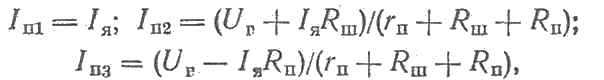
каждое из которых справедливо при наличии обмотки последовательного возбуждения только в одной цепи.
Соответственно зависимость ЭДС от силы тока якоря определяют по одной из следующих зависимостей:
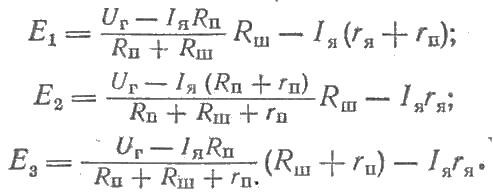
Частоту вращения п при заданной силе тока якоря находят по формуле n = Е/ФсE, где Ф — магнитный поток двигателя; сЕ — коэффициент пропорциональности напряжения.
Для получения уравнений в относительных единицах введем следующие базисные величины: nб = nном; Iб = Iном; Еб = Uном; Фб = Фном; Rб = Rном. Используя соотношения
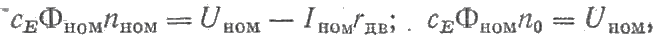
можно записать nном/nо = с’Е, в котором
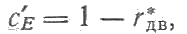
где rдв = rя + rп; n0 — частота вращения при идеальном холостом ходе.
Тогда формулу для определения частоты вращения в относительных единицах запишем так:
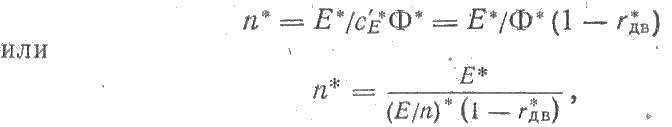
так как в относительных единицах Ф* = (Е/п)*.
Магнитный поток Ф* для соответствующей силы тока якоря при известной МДС главных полюсов (F* = F*пар + F*п) определяют по универсальным нагрузочным характеристикам. Нагрузочной характеристикой называют зависимость (Е/n)* = f (F*) при постоянной силе тока якоря I*я. Так как вид нагрузочных характеристик зависит от силы тока якоря, то они изображаются в виде семейства кривых, построенных при различных значениях Iя. Характеристика при Iя = 0 является кривой намагничивания двигателя.
На рис. 2.13 показаны универсальные характеристики двигателей серий ДП и Д. Характеристики изображены в относительных единицах. За базисные величины приняты номинальная МДС главных полюсов двигателя при ПВ = 25 % и номинальный магнитный поток Ф главных полюсов при протекании по якорю двигателя тока номинальной силы при ПВ — 25 % в направлении, соответствующем двигательному режиму. Типовые нагрузочные характеристики соответствуют действительным нагрузочным характеристикам конкретных двигателей серий ДП и Д, отличаясь от характеристик, полученных на основе опыта, на 2—3 %.
Электромагнитный момент двигателя (в Н?м)
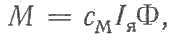
где cM — коэффициент момента.
Вращающий момент на валу двигателя отличается от электромагнитного на величину, определяемую механическими потерями и потерями в железе якоря. Таким образом, вращающий момент на валу двигателя может быть представлен в следующем виде:
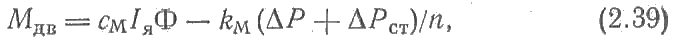
где ?Р — потери мощности на трение; ?Рст — потери мощности в стали; kM— коэффициент пропорциональности моментов.
Параметр ?M* = kM* (?P* + ?Р*ст)/n* определяют по кривым, выражающим зависимость ?M* = f (Е/n)* при различных постоянных значениях частоты вращения n*. Такие кривые, построенные в относительных единицах, показаны на рис. 2.14.
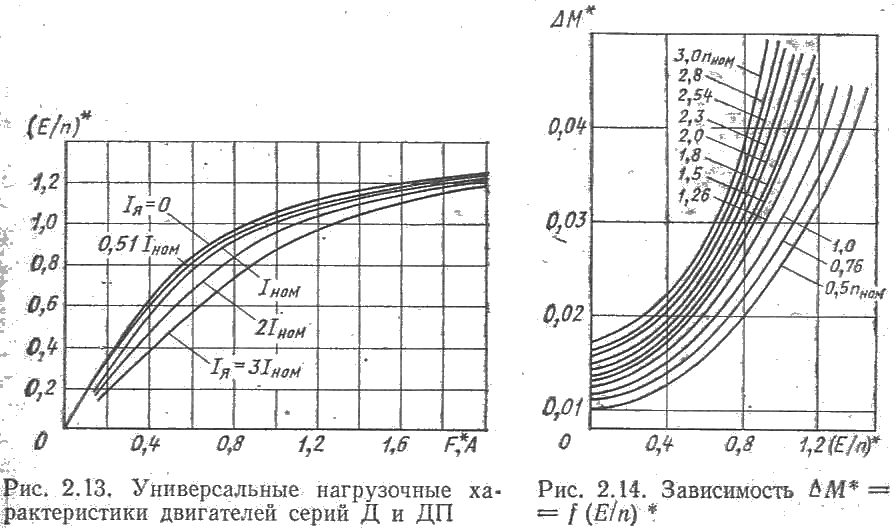
Пользуясь этими кривыми, нетрудно найти момент ?М* при различных магнитных потоках главных полюсов и частотах вращения. Коэффициент момента сM можно определить, исходя из того, что при базисных силе тока, магнитном потоке и частоте вращения вращающий момент на валу двигателя также должен быть равен базисному (номинальному). Следовательно, пользуясь выражением (2.39), можно написать, что при Мдв = Мб = Мном т. е.
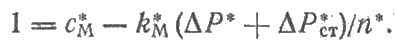
Определив по рис. 2.14, что для (Е/n)* = 1 и n* = 1 ?М* = 0,03, найдем
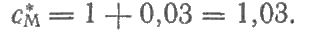
Окончательно формула для определения вращающих моментов на валу имеет вид
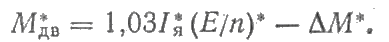
Источник: //vdvizhke.ru/jelektrodvigateli/kranovye-jelektrodvigateli/raschet-mehanicheskih-harakteristik-jelektrodvigatelej-postojannogo-toka.html
